Post-Newtonian N-body dynamics

The majority of codes for relativistic N-body simulations fail to take all known first post-Newtonian order terms in the equations of motion into account for computational reasons. Will (2014) showed that in some cases, for instance hierarchical systems or systems with a central massive object, some of the neglected terms are of similar or even higher importance than the terms that are taken into account, and he provides a way to efficiently calculate the relevant neglected terms, called cross-terms. We evaluate his method and provide expressions for the cross-terms in the case of multiple massive objects, yielding terms of similar algorithmic complexity.

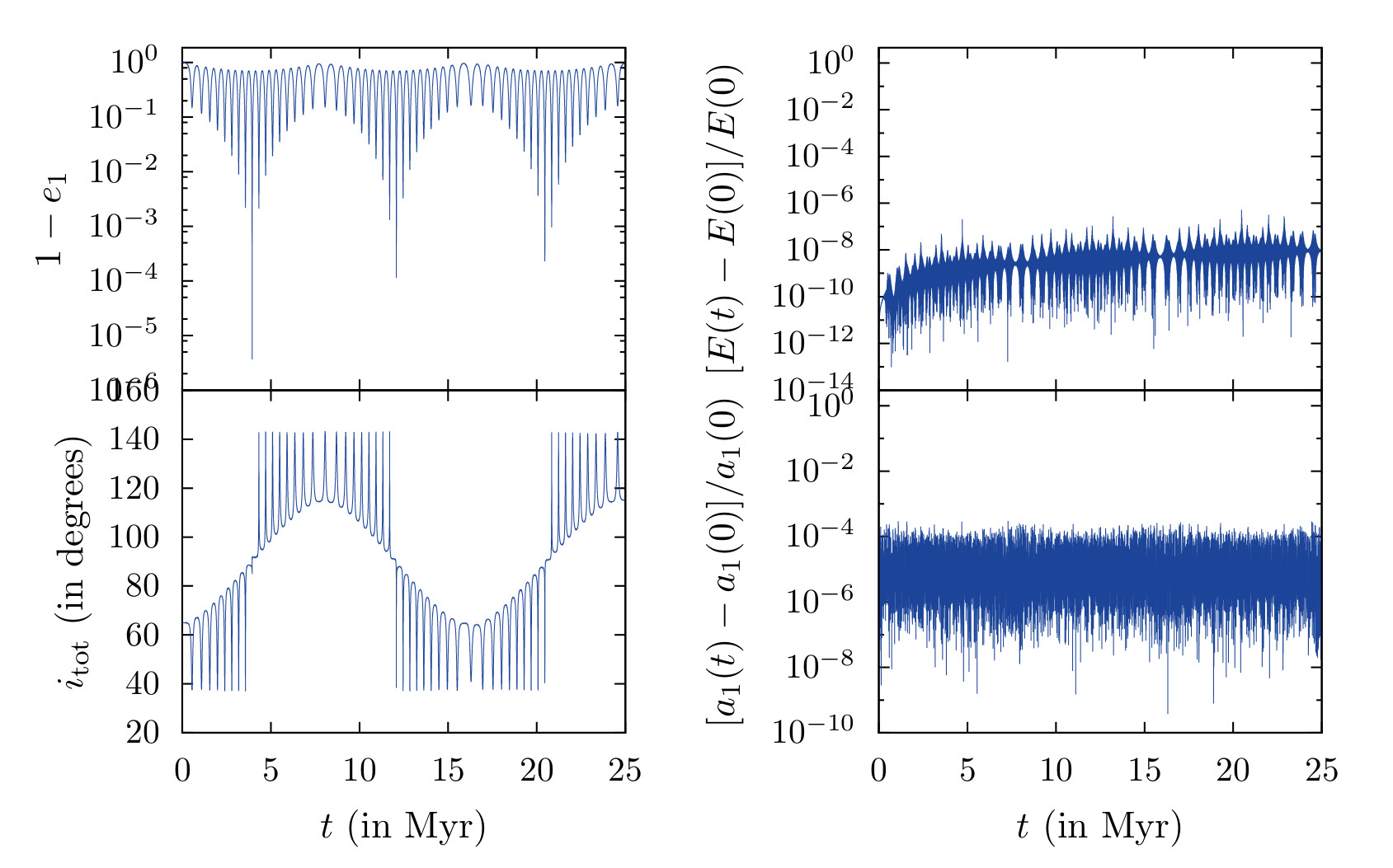
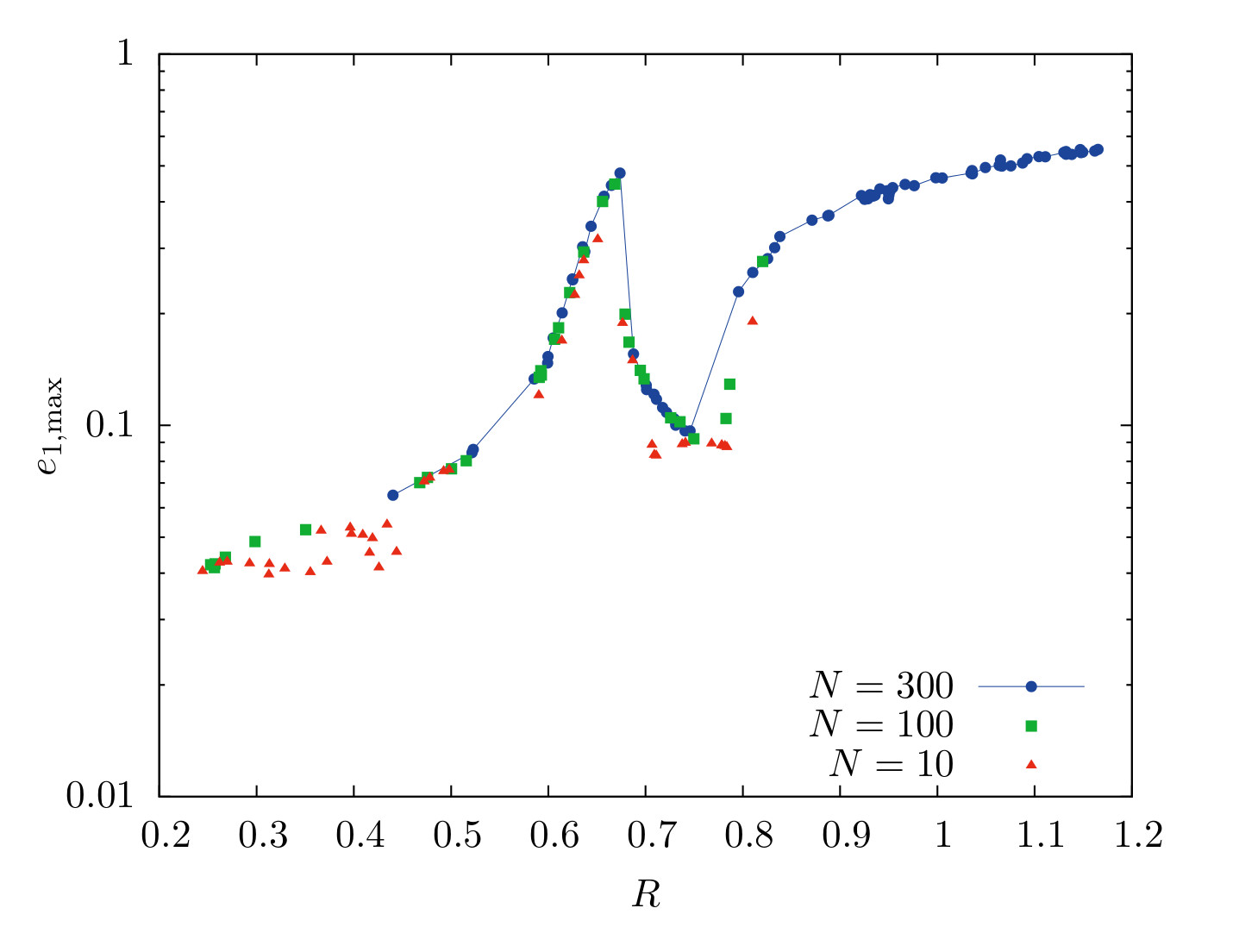
We use the Hermite integration scheme and Kustaanheimo-Stiefel regularization in the quaternion formation to numerically integrate the full first post-Newtonian equations of motion, in order to investigate the importance of the neglected terms. The code was validated using both two-body and hierarchical triple systems, reproducing the osculating elements derived analytically using Lagranges planetary equations, and the resonant eccentricity excitations, induced by post-Newtonian effects, recently obtained using purely secular orbital averaging methods by Naoz (2013). We however failed to reproduce their results for eccentric Kozai mechanism induced purely by post-Newtonian effects, instead of the usual Newtonian octupole variations, casting doubt on the existance of such a mechanism.